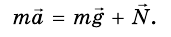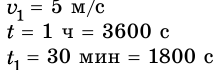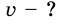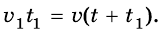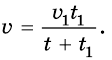Учебники
Журнал «Квант»
Общие
§4. Основные законы динамики
В предыдущем разделе «Кинематика» мы рассмотрели математические способы описания механического движения. Фактически мы занимались математикой — переводом расплывчатого словесного описания на точный и однозначный язык математических формул, функций, графиков и.д. Сейчас нам предстоит выяснить физические причины, приводящие к тому или иному виду движения, раздел механики, изучающий причины движения и его изменения называется динамика.
4.1 Закон инерции. Принцип относительности Галилея.
Повседневный жизненный опыт показывает, что для того, чтобы какое либо тело двигалось, к нему необходимо прикладывать определенные усилия [1] — для передвижения человек и животные используют свои мышцы, все средства транспорта снабжены двигателями, если не подталкивать скользящую по льду шайбу, то она останавливается, вы можете без труда продолжить этот ряд примеров. Поэтому складывается впечатление, что причиной движения тела является воздействие на него других тел. Такая точка зрения господствовала в научных представлениях человечества в течение полутора тысяч лет.
Приходилось даже придумывать экзотические объяснения для объяснения простых движений. Так, например, для объяснения полета стрелы, выпущенной из лука, была придумана такая замысловатая теория. Стрела движется в воздухе, воздушная среда перед стрелой является более разряженным, а позади нее более плотным, и именно этот более плотный воздух постоянно подталкивает стрелу в полете [2] .
Однако посмотрим на движение с иной точки зрения, попытаемся более подробно рассмотреть результаты воздействия одного тела на другое.
Пусть некоторое тело, например, тяжелый металлический шар, падает с некоторой высоты на поверхность земли. Он начинает двигаться под действием притяжения к земле, в ходе падения его скорость возрастает. Экспериментально можно показать, что его движение можно описать как примерно равноускоренное. Чтобы уменьшить ускорение пустим этот шар по желобу, наклоненному под некоторым углом к горизонту. Качение такого шара, по-прежнему остается равноускоренным, но величина ускорения уменьшается по мере уменьшения угла наклона. Поэтому разумно предположить, что при движении по горизонтальному желобу ускорение станет равным нулю. Именно, ускорение, а не скорость! Иными словами, его движение будет равномерным, с постоянной скоростью. Конечно, со временем шар остановится, но его торможение можно объяснить действием сил сопротивления воздуха и сил трения.
Рассмотрим еще один пример. Толкнем шайбу по поверхности стола. Сдвинувшись на некоторое расстояние, она остановится, следовательно, она движется с уменьшающейся скоростью, с отрицательным ускорением. Заменим поверхность стола, гладкой поверхность льда. И сообщим шайбе ту же начальную скорость. В этом случае шайба пройдет до остановки гораздо большее расстояние. Следовательно, величина (модуль) ее ускорения будет меньше. Поэтому разумно считать, что причиной отрицательного ускорения является сила сопротивления со стороны поверхности. Если каким-либо образом исключить действие поверхности, то движение шайбы должно продолжаться бесконечно долго.
Во всех случаях, оказывается можно найти причину изменения (!) скорости — действие других тел.
Таким образом, можно утверждать, что при отсутствии воздействия других тел, тело продолжает двигаться с постоянной скоростью, сохраняет скорость своего движения. Свойство тел сохранять свою скорость называется инерцией, а свободное движение тел называют движением по инерции. Сформулированное утверждение в физике носит название закона инерции Галилея.
Отметим, что, когда говорят о движении с постоянной скоростью, подразумевают постоянство скорости, как по величине, так и по направлению. Вспомните, как трудно повернуть на гладком льду — не хватает внешних сил, способных изменить направление скорости. Говоря в дальнейшем о равномерном движении, мы будем подразумевать движение с постоянной скоростью, как по величине, так и по направлению.
С проявлением инерции мы постоянно встречаем в окружающем мире. При резком торможении автобуса, пассажиров «бросает» вперед — они продолжают двигаться с прежней скоростью. Если на стол положить лист бумаги, а на него поставить какой либо предмет, то можно резко выдернуть этот лист бумаги так, что сам предмет не сдвинется с места.
В разделе «Кинематика» мы неоднократно подчеркивали, что механическое движение относительно — имеет смысл говорить только о движении одного тела относительно другого. Поэтому, в формулировке закона инерции Г.Галилея мы упустили одну существенную деталь – относительно какой системы отсчета рассматривается движение. Не трудно привести пример системы отсчета, в которой закон инерции не выполняется. Пусть поезд начинает отходить ускоренно от вокзала, в системе отсчета, связанной с поездом, вокзал движется с ускорением, хотя явных взаимодействий, приводящих к изменению скорости вокзала не заметно.
Поэтому закону инерции Г.Галилея [3] следует дать иную интерпретацию: существуют такие системы отсчета, в которых тело движется равномерно, при отсутствии взаимодействия с другими телами. Такие системы отсчета называются инерциальными.
Пусть некоторое тело А движется равномерно и прямолинейно относительно некоторой системы отсчета XOY. В любой другой системе отсчета, которая движется относительно XOY равномерно, движение тела А будет равномерным (но, конечно, с другой скоростью). Следовательно, любая система отсчета, которая движется равномерно относительно какой-нибудь инерциальной системы отсчета, сама является инерциальной.
Вопрос о существовании инерциальных систем отсчета, на самом деле, не простой. Во многих случаях, в качестве инерциальной системы отсчета рассматривают систему отсчета, связанную с поверхностью земли. Строго говоря, эта система не является инерциальной, так как Земля вращается вокруг собственной оси, то есть движется с ускорением. Эта неинерциальность проявляется в целом ряде экспериментов: движении маятника Фуко, отклонением в полете снарядов, подмыве одного из берегов рек и других. Безусловно, эти эффекты малы, и при решении многих задач ими можно пренебречь, то есть считать Землю инерциальной системой. Аналогичные рассуждения можно применить и к другим более грандиозным системам, например, связанным с Солнцем или другими звездами. Поэтому, вопрос об инерциальности той или иной системы отсчета связан с той точностью, которая требуется для описания физических явлений.
Таким образом, закон инерции постулирует существование инерциальных систем отсчета. Далее, если не будет оговорено особо, мы будем рассматривать движение тел именно в инерциальных системах отсчета.
Источник
Инерциальные системы отсчета в физике — определение и формулы с примерами
Содержание:
Инерциальные системы отсчета:
Вы уже знаете, что движение и покой относительны. Если относительно одной системы тело находится в состоянии покоя, то относительно других систем отсчета тело может двигаться. Рассмотрим, например, шайбу, лежащую на ледовой площадке. Шайба находится в покое относительно льда (Земли), потому что влияние на нее Земли компенсируется влиянием льда. Но для хоккеиста, движущегося мимо шайбы прямолинейно и равномерно, она движется прямолинейно и равномерно в противоположную сторону. Таким образом, одно и то же тело (шайба) относительно одной системы отсчета (связанной с Землей) находится в покое, относительно другой (связанной с хоккеистом) движется прямолинейно и равномерно. Но хоккеист ударил по шайбе клюшкой (рис. 276).
В итоге очень непродолжительного действия клюшки шайба начинает двигаться, приобретая некоторую скорость. Интересно, что после удара, когда действие клюшки на шайбу уже прекратилось, шайба продолжает движение. Тем временем после удара влияние на шайбу других тел осталось таким же, как и до удара: как и раньше, действие Земли компенсируется действием льда, а клюшка, как и до удара, никакого влияния на движение шайбы не оказывает. Шайба после удара движется по прямой линии с почти постоянной скоростью, сообщенной ей в момент удара. Но шайба в конце концов остановится, хотя из опыта известно: чем более гладкими будут лед и шайба, тем более длительным будет движение шайбы. Поэтому можно догадаться, что если совсем устранить действие льда на подвижную шайбу (это действие называют трением), то шайба продолжала бы двигаться относительно Земли с постоянной скоростью без остановки.
Однако если бы рядом с этой шайбой, движущейся равномерно, двигался хоккеист с такой же скоростью, то относительно него (системы отсчета, связанной с ним) шайба находилась бы в покое. И в этом случае одно и то же тело в одной системе отсчета (Земля) движется прямолинейно и равномерно, относительно другой (хоккеист) — находится в покое.
Этот пример и много других, подобных ему, является проявлением одного из основных законов механики, который называют первым законом движения, или первым законом Ньютона.
Инерциальные системы отсчета
Существуют такие инерциальные системы отсчета, относительно которых тело, движущееся поступательно, сохраняет свою скорость постоянной, если на него не действуют другие тела (или действие других тел уравновешено).
Само явление сохранения скорости движения тела (в частности, состояние покоя) при компенсации внешних действий на тело называют инерцией. Поэтому первый закон Ньютона часто называют законом инерции. Повседневное выражение «движение по инерции» и означает движение тела с постоянной скоростью, когда действие других тел уравновешено.
В первом законе Ньютона речь идет о равномерном прямолинейном движении. Движение мы можем рассматривать только в какой-либо системе отсчета. Возникают вопросы: в какой же системе отсчета выполняется первый закон? Можно ли считать, что он выполняется в любой системе отсчета? Закон инерции выполняется не во всех системах отсчета.
Первый закон Ньютона дает возможность определить, является ли система отсчета инерциальной. Для этого следует выбрать какое-либо тело, для которого действующие силы уравновешены, и проследить за тем, как оно движется относительно системы отсчета, которая интересует нас. Если движение равномерное и прямолинейное (в отдельном случае — покой), то система инерциальна; если движение неравномерно — система неинерциальна.
Возникает вопрос: существуют ли строго инерциальные системы? Ньютон, формулируя закон инерции и включая его в основные законы динамики, утверждал этим, что такие системы отсчета в природе существуют. В действительности, если в природе имеет место закон инерции, то должна существовать и такая система отсчета, где он выполняется абсолютно строго, то есть инерциальная система отсчета. А если существует хотя бы одна такая система, то из этого следует, что их есть бесчисленное количество, потому что всякая система отсчета, движущаяся равномерно и прямолинейно относительно инерциальной, будет также инерциальной.
Чтобы выяснить связь между силой, действующей на тело, и ускорением движения тела, следует выполнить опыт. Для проведения опыта выбираем тело, действующее на все другие тела с одинаковой силой. Таким телом может быть растянутая или сжатая пружина, в которой действует сила упругости. От всех других сил сила упругости отличается определенной особенностью, она зависит только от того, насколько растянута или сжата пружина, но не зависит от того, к какому телу пружина прикреплена. Поэтому на любое тело, прикрепленное к пружине, растянутой на определенную длину, действует одна и та же сила — сила упругости пружины.
Поскольку сила одна и та же, то какая-то величина должна быть одинакова для всех тел, которые ускоряются этой силой. На опыте и выясним, что это за величина.
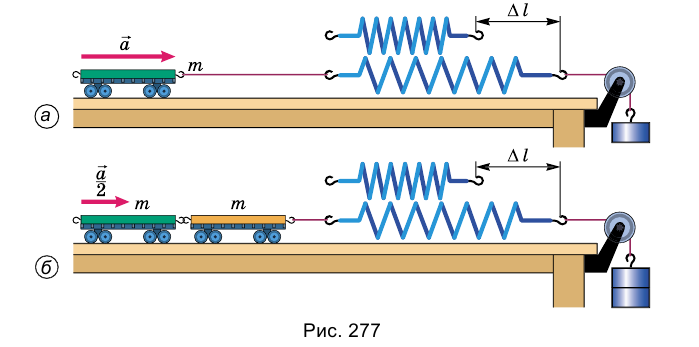
Опыт. К тележке, масса которой известна (т), прикрепим один конец пружины, а второй ее конец прикрепим к нити с грузом, переброшенной через блок (рис. 277, а). Вследствие притягивания к Земле груз движется вниз и растягивает пружину. Она, растянутая на определенную длину Д(, действует силой упругости на тележку и сообщает ему ускорение. Это ускорение можно измерить, например, оно равно а. 
Повторим опыт с двумя тележками одинаковой массы (их масса — 2т), соединенными вместе (рис. 277, б). Нам необходимо измерить ускорение тележек при том же удлинении пружины, поскольку сила должна быть неизменной. Чтобы удлинение пружины было таким же, как в начале опыта, следует подвесить к нити другой груз. Опыт показывает, что при том же удлинении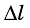 
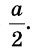
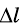
пружины ускорение двух тележек равно 
Если соединить три, четыре и больше тележек, то при том же удлинении 
пружины ускорения тел окажется в три, четыре и больше раз меньше, чем одной тележки. Оказывается, что с увеличением массы тележки в определенное число раз ускорение, которое приобретает тело при действии той же силы, уменьшается во столько же раз. А это значит, что одинаковым оказывается произведение массы тележки и ее ускорения.
Это дало Ньютону основание утверждать, что сила определяется произведением массы тела и его ускорения, и сформулировать важнейший закон механики, который назвали вторым законом Ньютона.
Сила, действующая на тело, определяется произведением массы тела и его ускорения, предоставленного этой силой.
Формулу, выражающую второй закон Ньютона, следует записывать в таком виде: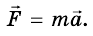 
Из этой формулы можно получить выражение для
ускорения движения тела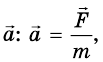 
из которого видно, что ускорение тела
всегда направлено так же, как и сила, вызывающая его.
Ускорение движения тела прямо пропорционально силе, приложенной к нему, и обратно пропорционально массе тела и направлено в сторону действия силы.
Следует заметить, что второй закон Ньютона, как и первый, выполняется лишь для материальных точек. В случае действия сил на протяженное тело второй закон описывает ускорение не всего тела, а только его центра масс. При поступательном движении тела все его точки имеют одинаковые ускорения. Второй закон выполняется для всех точек.
Каждый из законов Ньютона постепенно раскрывает содержание одного из важнейших понятий механики — понятия силы. Если второй закон утверждает, что любая сила вызывает ускорение, то третий закон говорит, что все силы имеют характер взаимодействий.
Силы, с которыми какие-либо два тела действуют друг на друга, всегда равны по модулю и противоположны по направлению.
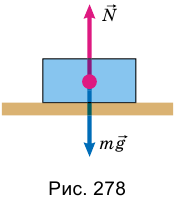
Пусть, например, на столе лежит тело (рис. 278).
С какой силой оно действует на стол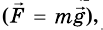 
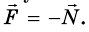
, с такой же по значению силой стол действует на тело N. Математически это записывают так: 
Знак «-» указывает на противоположность действия этих сил.
Третий закон Ньютона выполняется для подвижных тел
Однако равенство сил не всегда обусловлено третьим законом. Следует различать силы взаимодействия, приложенные к разным взаимодействующим телам, и так называемые равнодействующие силы, которые действуют на одно тело. Силы взаимодействия подчиняются третьему закону Ньютона, а силы, действующие на одно тело, подчиняются второму закону. Чтобы разобраться в этом подробнее, рассмотрим пример.
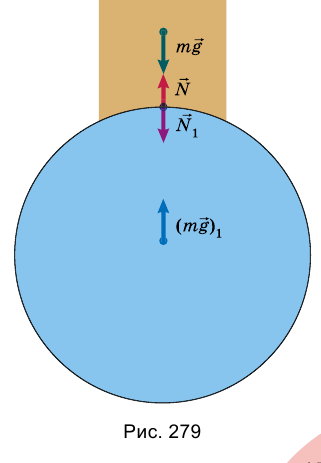
На поверхности Земли лежит тело (рис. 279). На тело действует сила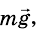 
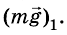
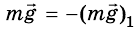
, с которой его притягивает Земля. Но по третьему закону Ньютона и тело притягивает к себе Землю с такой же по значению, но противоположно направленной силой 
Следовательно, 
по третьему закону Ньютона.
Кроме гравитационного взаимодействия Земли и тела, между ними существует еще и упругое: с какой силой тело действует на Землю, с такой же силой и Земля действует на тело, то есть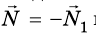
по третьему закону Ньютона.
Таким образом, на тело действуют две силы: mg и N. Для этих сил, поскольку они приложены к одному телу, можно записать второй закон Ньютона:
Тело находится в покое, то есть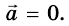 
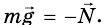
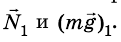
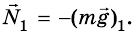
Поэтому 
Это равенство сил доказано на основе второго закона Ньютона. На Землю также действуют две силы: 
Они уравновешены, то есть 
Это равенство так же является следствием применения второго закона.
Пример задачи с решением
Велосипедист движется со скоростью 5 м/с. С какой скоростью двигался пешеход, вышедший из того же места на 1 час раньше, если велосипедист догнал его через 30 мин после начала своего движения?
Дано:
Решение:
Велосипедист и пешеход преодолели одинаковое расстояние, следовательно: 
сюда: 
Подставим значение известных величин и по-
лучим: и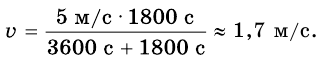
Ответ: 
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Энергия в физике
- Мощность в физике
- Взаимодействие тел
- Механическая энергия и работа
- Скорость при равнопеременном движении
- Перемещение, координата и путь при равнопеременном движении
- Криволинейное движение
- Ускорение точки при ее движении по окружности
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Источник
